Ai Pengya

The reason for introducing the t-test is because I think it is very important. Although many people may feel that it is not “useful”¹, I think this illustrates the basis for inferential statistics. I very informally taught this in my TA training class. The students told me it would be better to illustrate what the p-value is. However, I don’t have time, as each student only has 12 minutes to do the minor teaching. Sometimes, I think a t-test might be the most appropriate one to understand what inferential statistics is, which is the fundamental idea of t-test, ANOVA, regression, SEM, etc. Then you know why we need p-value and confidence intervals.

Usually, t-test is classified into one sample t-test, independent t-test, and paired t-test.

T-test is aimed to compare means:

• One sample t-test is to compare one mean with a number.
• Independent t-test is to compare two means from two different samples.
• Paired t-test is to compare means of the same variable in one sample.

I’m not going to talk about paired t-test here because it requires within subject data, which means the data of the same variable is collected from the same participant (e.g., pre/post test in experimental design, or longitudinal data). The idea would be similar to the independent t-test because it’s also comparing two means. The formula would be a bit different. But it doesn’t matter as we have many many software now. 😃

One sample t-test

I think one sample -test would be the best to know why we need inferential statistics. Frankly speaking, this question is equal to why we need p-value or confidence intervals to judge whether the hypothesis is supported or not.

As I mentioned, one sample t-test is to compare whether the mean of a variable is the same as (less or larger than) a number. For example, I measured environmental knowledge (range from 0 to 10) using a survey in China (Sample data download). The data is nationally representative. I want to know whether the environmental knowledge of Chinese is equal to 7 as I hypothesize it might be 7. Previously I have got the mean value of it, it’s 4.2432 (The steps in SPSS: Open SPSS -> Analyze -> Descriptive statistics -> Descriptives, then enter the variable you want to describe).

Looks like my hypothesis should fail because 4.23 is toooo far away from 7. But I cannot conclude it by this value alone. This is because the sample I got is only 1143 Chinese. Even though it is randomly selected from all the Chinese, it is not the Chinese population. Definitely we cannot measure all Chinese’s environmental knowledge. We can only get some people from the population. Then a question emerges: how could we know the population mean from the sample mean? It is very likely that if we get another 1143, the mean value is different. Therefore, maybe the mean of population is 7 – I got a mean of 4.23 only because I surveyed these people.

So how could I know if the population mean is not 7? A very smart idea come up by the statisticians is that we cannot know whether exactly the population mean is 7, but we can infer from the sample how likely the population mean is this number. We can get the likelihood or the probability that the population mean is 7, which is the idea of p-value.

(How to get such a probability is a bit complex question, I will continue to leave my tutorial simple. There are assumptions and formulas. Basically, you need to get the t statistic and compare it with t distribution. You can check some books or online sources for more details)

So in SPSS, I use Analyze -> Compare Means -> One-Sample T Test

Enter Environmental knowledge, which is my interested variable. And I change the test value into 7, which is I hypothesized.

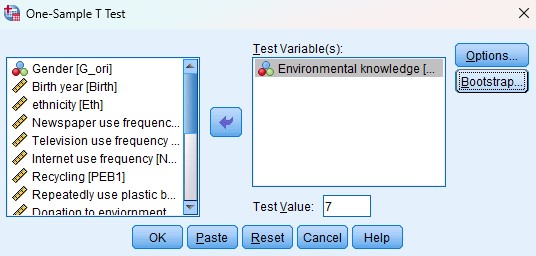
You can see the Sig. (2-tailed) for p-value, which means that “the mean = 7” only have a probability of 0.000 to happen. (Okay…just tell me it is impossible, lol.) Therefore, I can reject the hypothesis that the average environmental knowledge of Chinese is 7 (This is what we usually called H₀, or null hypothesis) because I found it is almost impossible that the average environmental knowledge of Chinese is 7 based on the p-value SPSS told me.

So is it possible that the mean environmental knowledge is 5? Looks like it might be okay because 5 is not very deviated from 4.24. So I can follow the same procedure except changing the testing value from 7 to 5 and I get the results.

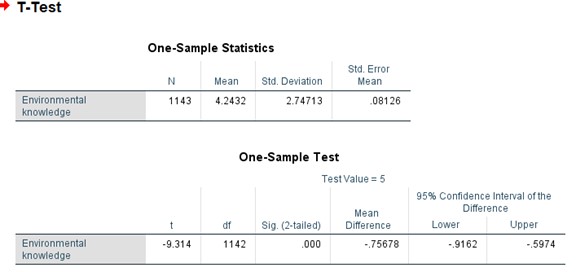
I was a bit surprised that “Mean environmental knowledge = 5” is also rejected. Anyway, based on the results, we should still reject this hypothesis. Then I tried 4.2 and the p-value is larger than the 0.05 criterion which is commonly used.

This time we can see the p-value = 0.595. So it is very likely that mean = 4.2 is likely to happen. At least we cannot 95% sure it is not true. Therefore, we can say we cannot reject mean = 4.2. However, we cannot conclude that the population mean is 4.2. We only get a probability that 4.2 is likely to be the possible population mean. (You definitely can see from this sample, 4.2432 is the most likely one. the p-value should be very close to 1.) And we can also only conclude that 5 and 7 is very very very unlikely to be the population mean. (But it still might be, we just don’t know from this sample.)

The selection of the 0.05 is due to the consideration of type I error. Of course there are many contradictions about such an arbitrary number. But anyway, under the current statistical framework, just remember if p-value < 0.05, reject the null hypothesis. For one sample t-test, the null hypothesis is the mean = the number you hypothesized.

BTW, just to mention a bit about the later content. For independent t-test, the null hypothesis is the two means are equal. So, reject the H0 means the two means are not equal. In other words, the means of the two groups are different.

For regression/mediation/moderation/SEM, the null hypothesis is the coefficient = 0. Thus, rejecting the H0 means the coefficient is NOT equal to 0. That is, there is relationship or the path/the mediation effect/the interaction effect is statistically “significant” (as it is highly likely that it’s not 0).

1. Actually, t-test is widely used to examine the significance of coefficients. But most of the time, it seems the work of the computer. For example, the coefficients of OLS regression are tested with a t-test. However, if you don’t know it’s examined by t-test, it does not affect you to use OLS regression. ↩︎