Ai Pengya

Original article: Rosenthal, S. (2017). Structural equation modeling. M. Allen (Eds.), The SAGE Encyclopedia of Communication Research Methods (pp. 1683-1687). Sage Publications. https://hdl.handle.net/10356/165157

结构方程模型（Structural equation modeling，SEM）可以用来做多种多元统计分析，包括多元回归，中介效应，条件而效应，方差和协方差分析。在传播学的研究中，SEM最常见的应用是验证性因子分析（confirmatory factor analysis，CFA）和路径分析（path analysis）。CFA可以通过许多观察变量确定一个或多个非观察变量，或称潜变量（latent variable）。CFA通常用来验证具有多个项目的指标或者量表。路径分析是用来估计结构点之间的相关和回归的路径系数，这些结构点可以是观察变量也可以是潜变量。当路径分析中包含潜变量时，确定这些潜变量的方式与CFA是一样的，即所谓测量模型（measurement model）。而潜变量和其他观察变量之间的路径就构成了所谓结构模型（structural model）。

SEM的构建是基于理论的。通过理论确定了需要估计的模型之后，软件通过数据的协方差矩阵进行估计。可以通过路径追踪法则（path tracing rules）手动估计（如果你真的愿意手算的话……）。SEM需要估计的参错包括相关系数，每条路径的回归系数，外生变量的方差，以及内生变量的残差。没有指定的路径系数就是被限制为0的（就是模型图里面那些没有连在一起的变量，没有指定它们之间的关系，相当于认为这些之间无关，路径系数为0）。用真实数据进行估计的时候，普遍而言如果模型中的限制（constraints）越多，那么估计出来的模型离理论模型的偏差就越大（这个其实也比较好理解，就是如果两变量之间的关系确实是0的话，不给它们加上这个限制，它们还是可以估计出来一个0。但是如果加上了限制，万一不是0，就偏离真实数据了）

既然用SEM估计理论模型不可能完全符合真实数据，所以需要一系列指标帮助判断模型的拟合程度（model fit）怎样，这些拟合优度的指标提供了模型在统计上是否良好的信息。这些指标侧重点不一样，一些侧重模型的简洁度（parsimony），一些是用来平衡第一类和第二类错误。

常用的SEM的指标有：

• 卡方值（chi-squared，χ2)
  • 检验真实数据得到的协方差矩阵与模型推导出的协方差矩阵之间的差异的指标。原假设是没有差异，所以p应该>0.05。但是因为这个指标对样本量非常敏感，一般当样本量>400的时候通常都会显著，所以并不是一个很准确的判断指标。
  • 两种方法解决这个样本量导致的问题：
    • 第一，可以用协方差矩阵，但是却确定一个较小的样本量，不管真正的样本量是多大。
    • 第二，可以用χ2/df。
  • 但是两个都有问题，因为第一个方法假定一个样本量太随意了，而第二个方法没有一个明确的标准判定其大小。
• 均方根误差（Root-Mean Squared Error of Approximation，RMSEA）
  • RMSEA是基于卡方和自由度的估计量，但是考虑了样本量的问题，所以这个指标对样本量不敏感。
  • 一般来说，RMSEA要<0.06，并且越小越好。另外其90%置信区间的上限最好不超过0.1。
• 比较适配度指标（Comparative Fit Index，CFI）
  • CFI是比较需要估计的模型得到的协方差矩阵和基准模型得到的协方差矩阵之间的差别。基准模型（baseline model）认为所有的变量之间都是无关的，所以一般来说基准模型的拟合度都是分会场差的，所以跟需要估计的模型相比，其卡方值通常比较高。
  • 一般来说，CFI越高代表着模型估计越好。通常CFI应该>0.95。
• 标准化均方根残差（Standardized Root Mean Square Residual，SRMR）
  • SRMR直接估计残差的协方差矩阵。因为残差越小=模型拟合度越好，所以SRMR越小越好。
  • 一般而言，SRMR需要<0.08
  • 当CFI约为0.96且SRMR约为0.09时，第二类错误的概率最小并且第一类错误的概率可以接受。另一个平衡第一类和第二类错误的组合是RMSEA约为0.06且SRMR约为0.09
• 相对的拟合度
  • 除了比较单个模型，拟合优度（goodness of fit）也可以通过比较不同的模型来判断。
  • 一种方式是比较嵌套和非嵌套模型，通过比较卡方值变化和自由度的变化以及相对应的p值，可以判断限制（restricted）的模型是否更好（如果卡方值显著减小）。
  • 对于非嵌套模型，卡方值是不适用的，这时候可以用其他的一些指标，比如赤池信息准则（Akaike Information Criterion，AIC），贝叶斯信息准则（Bayesian Information Criterion，BIC），和调整后贝叶斯信息准则（sample-size adjusted BIC，SSABIC)。一般而言这些指标越小的模型越好。
• 修正指标（Modification Indices
  • 大部分结构方程模型的软件都会提供修正指标。修正指标所提供的信息是当解除特定参数的限制之后的卡方值变化。一般标准是一个自由度的卡方值在3.84的时候显著，所以如果解除一个参数的限制（也就是增加了一个自由度）能够让卡方值增加3.84以上，也就可以让模型的拟合度更好。
  • 但是并不能通过修正指标来决定是否增加某个可以自由估计的参数（也就是解除这个参数的限制），因为结构方程模型是需要通过理论推导。所以只有那些符合理论的那些参数（比如说某两个变量之间的路径是否增加）可以进行调整。当研究者根据修正指标增加路径的时候，模型的自由度会下降。

其他的一些SEM有关概念：

• 嵌套和非嵌套模型（Nested and Non-Nested Models
  • 如果模型1可以通过限制某些参数得到模型2，那么就说模型2嵌套于模型1（model 1 is nested within model 2）
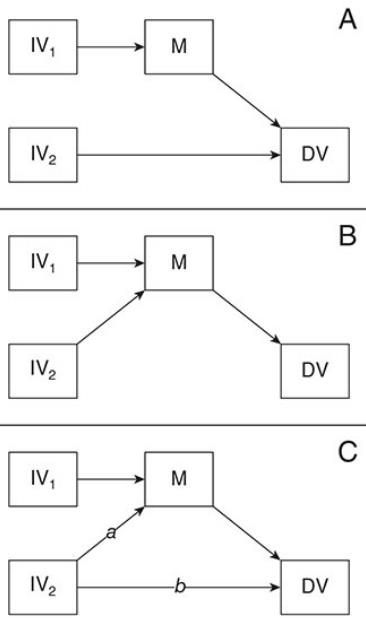
  • 例如以下这三个模型，A和B是非嵌套模型，因为A和B不能通过限制某些参数相互转换，它们之间的比较只能通过AIC和BIC这些。但是A和B都嵌套于C，A可以通过限制C中的a=0得到，B可以通过限制C中的b=0得到。所以A可以与C通过卡方进行比较，B也可以与C通过卡方进行比较。
  • 
• 模型的识别（Model Identification）
  • 结构方程的估计需要模型是过度识别（over-identified, df>0）或恰好识别（just identified，df = 0)。如果模型识别不足（under-identified，df<0），那么模型无法估计（简单的理解就是没有自由度，需要估计的参数超过了数据所能估计的上限）。
  • 如果模型中一共有k个变量，那么观察得到的参数的个数是[k*(k + 1)]/2。而模型需要估计的参数包括模型设定的共变系数，回归系数，外生变量的方差，内生变量的残差。
  • 例如上图的模型ABC都一共有10个观察得到的参数（所有两个不同变量之间的协方差（6个）以及所有变量自己的方差（4个））。A和B需要估计7个参数（3个路径系数（就是回归系数），两个方差（IV1和IV2两个外生变量，就是没有被箭头戳中的），两个残差（M和DV两个内生变量，就是被箭头戳中的），所以A和B的df=10-7=3。而C增加了一个需要估计的路径系数，所以C的自由度减少1，就是df=2。
  • 一个识别不足的例子是一个只有两个items的潜变量。这个模型只有3个观察到的参数（Item 1和2的方差以及它们之间的协方差）
• 样本量
  • 一般的准则是每个测量的item需要有至少10个样本。另一个建议是每个需要估计的参数至少有5个样本。样本量的选取依赖于所需要的统计功效（statistical power）以及模型拟合度指标。有一些在线的工具或软件可以用来计算样本量（比如R和G*Power）。
• 验证性因子分析（CFA）
  • Notes：发现到现在还没有解释潜变量是什么的文字，感觉这是理解SEM的基础，就在这里补充一下了。
  • 根据我的理解，很多测量，尤其是心理学的测量，是无法得到真正的对某个变量的测量。比如说幸福，态度，行为意愿等等，只能通过问参与者一些问题，比如你是不是开心，是不是幸福这样的——这些问题看似在直接问幸福感，但其实它们表示的还是一个很显性的东西，也就是人们说出来的话。那么怎么知道人们的幸福到底是怎样的呢？潜变量的逻辑就是，比如幸福这个潜变量，如果人们感到幸福，那么就会导致他回答他很幸福/开心/高兴这样的一系列问题，所以我们可以通过他们外显的这些回答去反向推导他内心真实的幸福感。所以真实的幸福感是无法测量的，但是因为我们认为这个幸福感导致了那些我们可以测量的东西，所以SEM就通过这些外在的测量得到的东西去反推这个潜变量这样一个“潜在的”的变量。这也是为什么潜变量的箭头指向是有点反直觉的，是从潜变量出发指向观察得到的items，这里面就是暗含latent variable构建的逻辑。
  • CFA是相对于探索性因子分析（Exploratory factor analysis，EFA）而言的。EFA顾名思义就是探索性的，通过观察得到的数据（有点像聚类一样）探索可能存在的潜变量。而CFA就是从理论确定了哪几个items可以构成一个潜变量，然后构建这个模型确定是不是这样。
  • CFA基本上与测量模型是一样的。一个最基础的CFA分析，一个因子，三个indicators：
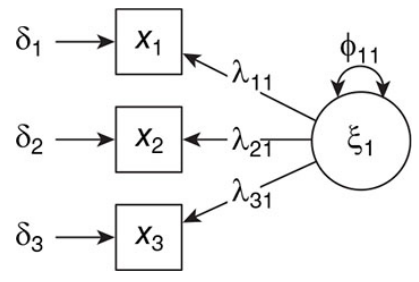
  • λ是因子载荷（factor loading）。以上这个模型是恰好识别的：一共有3个观察到的变量（潜变量不是一个真实存在的东西，所以它本身无法提供可以用来估计的数据，它自己反倒是需要通过x1，x2，和x3的数据进行估计），所以提供的观察到的数据信息有6个（3个x1-3的方差，3个x1，x2，和x3两两之间的协方差）。而需要估计的参数也恰好是6个（2个因子载荷（有一个被默认为1，否则无法估计），三个观察变量x1，x2，和x3的残差，还有潜变量的方差）
• 结构方程模型（SEM）
  • SEM的优势就在于可以同时估计多个回归方程还可以包含潜变量。
  • 测量模型（measurement model）：在估计结构模型前，需要先估计测量模型。测量模型将所有的潜变量的协方差都作为自由估计的参数。如果测量模型的拟合度不好，那么就得通过一些方法增加模型适配度，比如去掉一些项，增加cross-loading，增加残差相关之类。
  • 结构模型（structural model）：结构模型包含因子之间的结构，以及与理论相匹配的路径。如果结构模型的适配度良好，那么就可以得出关于变量间关系的结论了。
  • 路径分析（path analysis）：有时研究者会用已经是很成熟的量表，这时候他们的关注点只在变量之间的关系上。这个时候可以只做结构模型，将item直接组合成变量（比如求均值）。这样的模型不包括测量模型，只有变量之间的路径。除了SEM可以做路径分析，研究者也可以用多个回归模型去做，然后在用路劲追踪准则去算适配度。但是更简单的方法当然是直接用SEM去算，直接得到模型适配度。